【ほぼ失敗】遭難者を襲う「正常性バイアス」を体感出来るテスト

こんにちは、寝袋！です。

私は山を案内する人間の端くれとして、登山者の安全とか遭難予防に興味があります。

そのため、遭難事故や安全対策について、自分なりの意見をこれまで書いてきました。

みなさんも遭難体験の手記などを読まれたことがあると思いますが、こう思いませんか？

「なんでそんな馬鹿なミスしちゃうかなあ？　ちゃんと考えればいいのに」

でも、実際に遭難に陥りそうになっている人は、正常な判断ができない状態と言われています。

その大きな要因の一つが、「正常性バイアス」というものです。

今回は、みなさんにあるテストをやってもらいたいと思います。

そんなに難しいものではありませんし、時間もかかりません。

あなたを「正常性バイアス」に支配させるテストです。

これに合格する人は、きっと遭難しそうな危機でも、冷静に判断・行動できる人です。

でも、おそらく95%の人が失敗するんじゃないかな？

さあ、あなたはどうでしょうか？

遭難事故の原因の一つ「正常性バイアス」とは？

誰でもおちいります

正常性バイアスとは、「自分なら大丈夫」とか「正しいはず」とか、自分に都合の良い情報だけを信じて、行動してしまうことです。

道に迷っているのに「もう少し先へ行ってみよう」と考えたり、「迷っちゃったけど、下っていけばきっと降りられる」とか判断してしまうんですね。

第三者の目で見れば、「なんでそんなことしちゃうかな？」と思いますが、そう考えてしまう恐ろしい「力」が正常性バイアスです。

実際に体験することが出来ます

じつのところ、私も時々経験します。

「たぶん大丈夫」と思う気持ちは、誰にでもあるものだと思います。

でも、

「わかってるって。それでも自分は大丈夫さ」

と思っちゃってるわけですから、歯止めが効きません。

そこで、

「自分も例外じゃなく正常性バイアスに支配されることを体験しておけば、いざという時に冷静になれるかも？」

と考えて、今回のテストを書いてみました。

登山者のみなさん、面白い（？）からぜひやってみて！

「正常バイアス」体感テスト

テストのルール

それでは、「正常バイアス体感テスト」の方法とルールを説明しますね。

というテストです。

本当は、あなたと私が面と向かってやるのがいいんですが、そういうわけにもいきません。

そこで、ある程度私が想定した流れで、進めていきたいと思います。

そして最後に、私がテスト結果を発表します。（面と向かってなくても出来ます･･･フフフ）

では、実際にやってみましょう！

テスト開始！

それでは「バイアス体感テスト」スタートです。

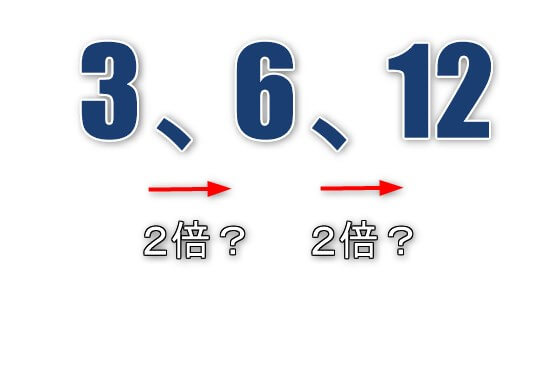
さて、これからあなたは数字を3つあげて、あなたが推測した法則を検証していきます。

対面していれば何でも自由なのですが、都合上、最初の数字を「4」でやってみましょう。

どうですか？

おそらく多くの人が『4、8、16』と言ったんじゃないですか？

第一印象では「倍々になってるのかもしれない」というのが浮かびますからね。

いいでしょう、私の答えは「法則に合ってます」です。

では、次は最初の数字を「5」でやってみたらどうでしょう？

さきよりもっと多くの人が、自信を持ってこういいますよね？

『5、10、20』と。

私の答えはやっぱり「法則に合ってます」です。

「６だったら『6、12、24』」

でも「法則に合ってます」ですし、

「1だったら『1、2、4』」

「2だったら『2、4、8』」

でももちろん「法則に合ってます」と答えます。

かんたんですね？　では、あなたの考える「ある法則」とは？

「おいおい、念のためにもっと検証したいぞ！」

と思った人は、慎重ですね。

でも、対面してテストできない以上、そこは我慢してください。

ただ、その試してみたい検証は、あとで大事になるので覚えておいてくださいね。

答えは「どんどん2倍になる」？

ほとんどの人が同じ回答に行き着いたと思います。

カンの鋭い人なら、2つ目『4、8、16』あたりで確信していたでしょうね。

慎重な人でも、3つか4つ検証すれば「間違いない」と思ったでしょう。

「どんどん2倍になっている」

こう答えた人は、じつは間違いです。

これらの数字に秘められた法則は、なんと、

「左の数字より右の数字が大きい」

つまり、

「○<○＜○」

です。

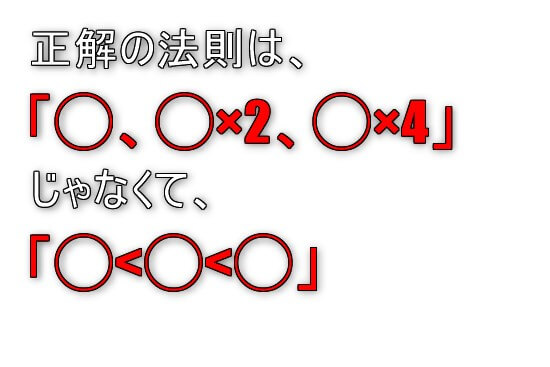
めちゃくちゃシンプルで、小学生でもわかる法則です。

「バカにしやがって！　そもそも、倍々だって法則になってるじゃないか！」

と怒った人もいるかもしれません。

でも、違いますよ？

あなたが検証したくて（都合上）検証出来なかった数字に、

「4、5、6」

はありましたか？

「4、7、8」

はどうでしょう？

私はそれらを言われたら、「法則に合っています」と答えたんですよ？

たぶんそこであなたは、

「ええー！　合ってる？　倍々じゃないのか？」

と気づいたでしょう。さらにもし、

「4、3、5」

と言われたら、「それは法則に合っていません」と答えました。

どうでしょう？

「倍々になる」なんて法則は、まったく検討違いだということがわかってもらえると思います。

このテストは、

「わざと間違った数字で検証しようとした人」

だけが正解にたどり着けるのです。

テストの意味

とはいっても、ちょっと意地悪なテストですし、なにより私が文面で誘導した面もありますし、対面してやったわけでもありません。

でも、

「おっ、2倍2倍で合ってる？　それならこれは？　やっぱり？　じゃあ、2倍2倍でファイナルアンサー！」

と安易になった場合は、すでに「正常性バイアス」に支配されていました。

「まてよ？　何回でも検証していいんだから、念の為に、『わざと違う数字』を言って確認してみようかな？」

と考えた人だけが、正常性バイアスに支配されていなかったのです。

もしかすると、「小学生でもわかります」なんて言葉があるのも、あなたの中に油断を生んだ影響もあるでしょう。

「よーく考えてね」って書いてあったら、もう少しは慎重に考えたかもしれません。

「正しいと思うんだけど、もしかすると違う可能性もあるな」

「たまたま一致してるだけかもしれない」

と考えることが必要だったわけです。

山だったら･･･

これが山だったら、どんな感じでしょうか。

「なんだか踏み跡がなくなったけど、でも、分岐点なかったし合ってるよな」

「みんなこっちへ行ってるから、きっと同じところにつながってるんだな？　私もこっち行こう」

分岐点はなかったのではなく見逃しただけかもしれないですし、みんなが行くのは違うルートかもしれません。

「もしかして分岐点見逃したかも。踏み跡があるところまで戻ってみよう」

「みんなは違うルートなのかもしれない。調べてきた予定通りに進もう」

と考えるほうがいいでしょうね。

正常性バイアス体験テストの結果について

あなたの結果はどうでしたか？

はっきり言って、こういう文章形式でテストしたので、ほとんどの人が私の誘導とひっかけにかかってしまったと思います。

テストに合格したか、失敗したか、じつはそこは重要ではありません。

失敗しちゃった人が、

「あら、自分だってそうなっちゃうのか。これが正常性バイアスか」

と感じてくれたら、それでいいなと思います。

なんか偉そうにテストとか言ってすみませんでした。

ほんとうは、山の楽しさとか、道具の紹介とかだけ書きたい（書くのもそっちが楽しい）のですけど、やっぱりね、最低限の安全対策を身に着けてこその楽しさと思いますので。

山では正常性バイアスがパワーアップして襲ってきます。

それに負けず、しっかりと山を楽しんでいきましょう。

【生存性バイアス】私達はまだ遭難の本当の原因を知らないのかも